量子计算机演示教程
第四节:量子纠错码
量子纠错码可以利用量子操作门进行编码,编码线路为(图4-2:arXiv:quant-ph/9705052)。此纠错码用5个量子比特来代表一个逻辑比特,对三种错误
\(X,Y,Z\)都可进行纠错。

量子模拟器复现出来的具体线路为:
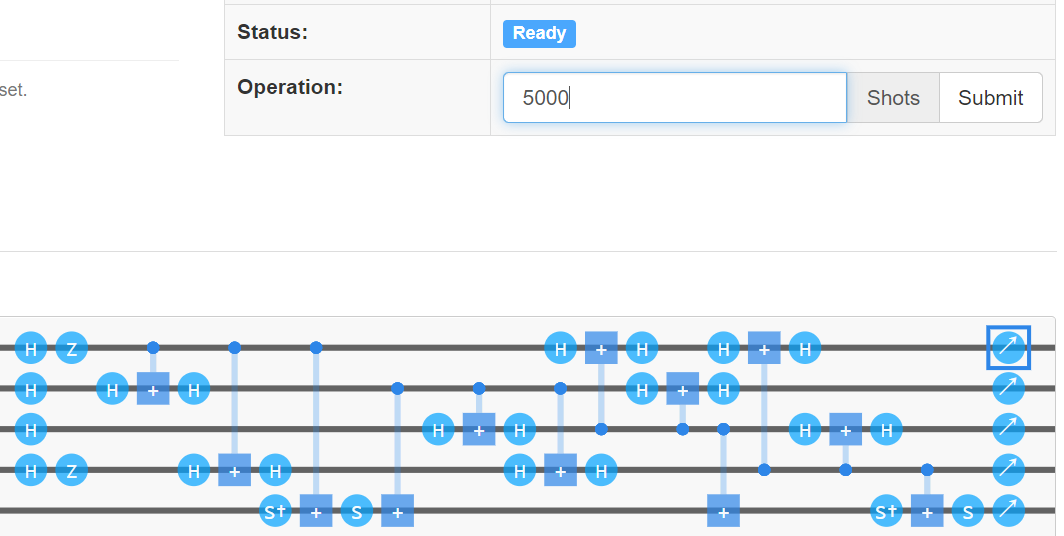
(图4-1)
线路计算结果为:

(图4-2)
这个结果和下面编码公式完全一致:
\(
\begin{aligned}
\ket{\bar{0}}=&\ket{00000}+M_1\ket{00000}+M_2\ket{00000}+M_3\ket{00000}+M_4\ket{00000} \\
&+M_1M_2\ket{00000}+M_1M_3\ket{00000}+M_1M_4\ket{00000} \\
&+M_2M_3\ket{00000}+M_2M_4\ket{00000}+M_3M_4\ket{00000} \\
&+M_1M_2M_3\ket{00000}+M_1M_2M_4\ket{00000}+M_1M_3M_4\ket{00000} \\
&+M_2M_3M_4\ket{00000}+M_1M_2M_3M_4\ket{00000}\\
=&\ket{00000}+\ket{10010}+\ket{01001}+\ket{10100} \\
&+\ket{01010}-\ket{11011}-\ket{00110}-\ket{11000} \\
&-\ket{11101}-\ket{00011}-\ket{11110}-\ket{01111} \\
&-\ket{10001}-\ket{01100}-\ket{10111}+\ket{00101},
\end{aligned}
\)
如果第5个量子比特为
\(1\), 则编码结果应该显示为逻辑\(1\)的纠错码,量子线路只是在第5个量子比特添加\(X\)门即可。线路和计算结果为:

(图4-3:第5个量子比特增添了\(X\)逻辑门)
计算结果为:

(图4-4)
和我们需要的逻辑比特完全相符:
\(
\begin{aligned}
\ket{\bar{1}}=&\bar{X}\ket{\bar{0}} \\
=&\ket{11111}+\ket{01101}+\ket{10110}+\ket{01011} \\
&+\ket{10101}-\ket{00100}-\ket{11001}-\ket{00111} \\
&-\ket{00010}-\ket{11100}-\ket{00001}-\ket{10000} \\
&-\ket{01110}-\ket{10011}-\ket{01000}+\ket{11010}.
\end{aligned}
\)
考虑需要编码的量子比特为\(\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\),则计算结果应该是32个基等振幅的叠加,线路为第5个量子比特开始后施加Hadamard门,线路和结果为:
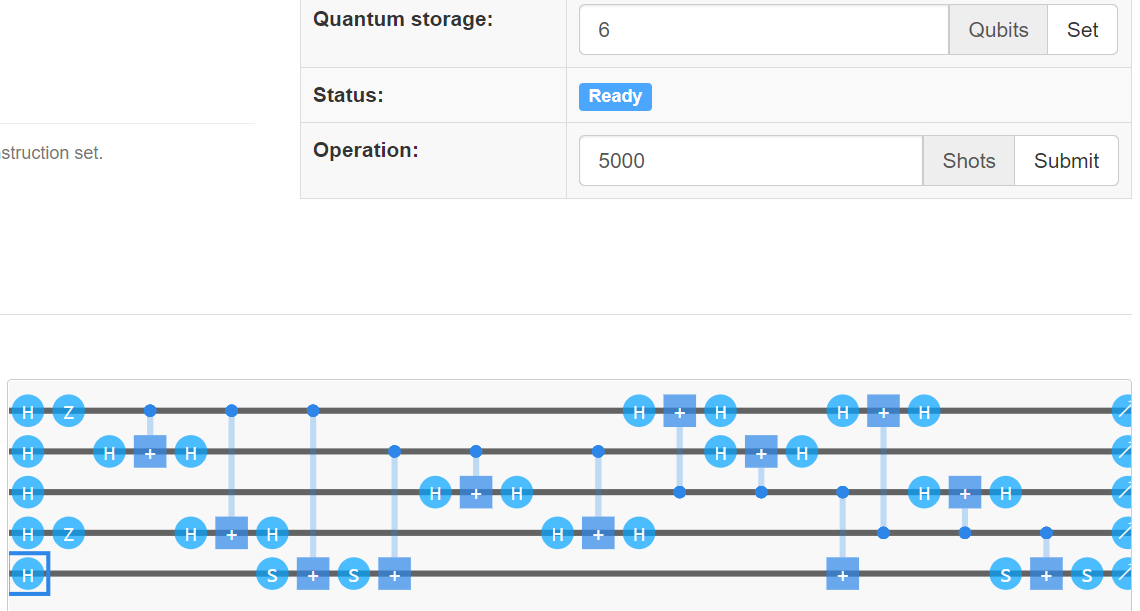
(图4-5:被编码的量子比特为叠加态)

(图4-6:计算结果为32个基的等几率叠加)
可以考虑其它的叠加态比如
\(\frac{\sqrt{3}}{2}\ket{0}+\frac{1}{2}\ket{1}\)被编码为纠错码,即第5个量子比特绕Y轴旋转\(\frac\pi3\),进行计算后,几率应该相互比例为1:3. 线路和计算结果如下:

(图4-7:入态被逻辑门\(Ry\)旋转了\(\frac\pi3\))
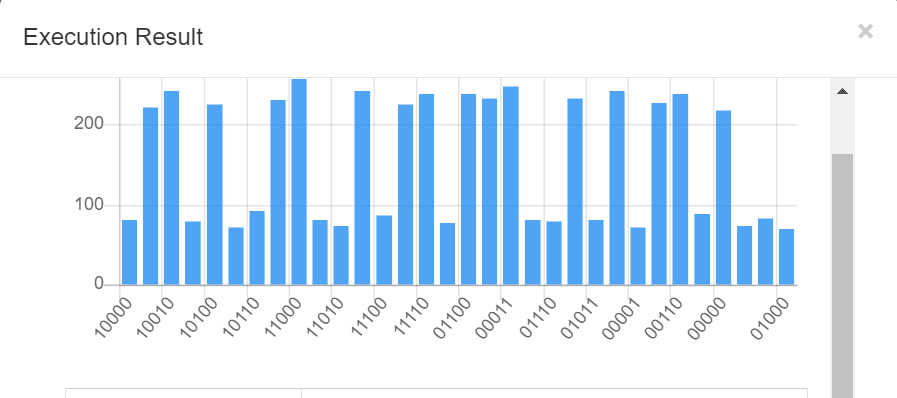
(图4-8:计算结果显示32个基的振幅分为两种,几率比为3:1)
结果符合预期。